|
|
|
Объем треугольной пирамиды
|
|
Объем треугольной пирамиды
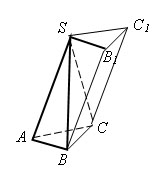
Пусть SABC – треугольная пирамида с вершиной S и основанием ABC. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма составлена из трех пирамид: данной пирамиды SABC и еще двух треугольных пирамид SCC1B1 и SCBB1.
У второй и третьей пирамид равные основания - ΔCC1B1 и ΔB1BC и общая высота, проведенная из вершины S. Поэтому у них равные объемы.
У первой и третьей пирамид тоже равные основания - ΔSAB и ΔBB1S и совпадающие высоты, проведенные из вершины C. Поэтому у них тоже равные объемы.
Значит, все три пирамиды имеют один и тот же объем. Так как сумма объемов равна объему призмы, то объемы пирамид равны SH/3.
Объем любой треугольной пирамиды равен одной трети произведения площади основания на высоту:
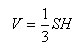
|
| |
|
|