|
|
|
Виды алгебраических уравнений
|
|
Виды алгебраических уравнений
anxn + an-1xn-1 + ... + a1x + a0 = 0. - Алгебраическое уравнение n-й степени общего вида.
Пусть коэффициенты ak - действительные либо комплексные числа.
1. Для краткости, обозначим левую часть уравнения, которая является полиномом степени n, следующим образом:
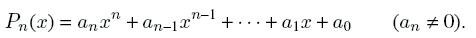
Число x = ξ называется корнем уравнения, а так же корнем полинома Pn(x), если Pnξ = 0.
Число x = ξ называется корнем кратности m, если Pn(x)=(x=ξ)mQn-m(x), где
m - натуральное число, 1 ≤ m ≤ m и Qn-m(x) - полином степени n - m, такой, что Qn-m(ξ) ≠ 0.
2. Основная теорема алгебры. Алгебраическое уравнение n-ной степени имеет в точности n корней (действительных
или косплексных), причем корни кратности m встречаются ровно m раз.
3. Если алгебраическое уравнение имеет корни x1, x2, ..., xs, кратностей k1, k2, ..., ks
(k1 + k2 + ... + ks = n), то левая часть уравнения может быть представлена в виде:
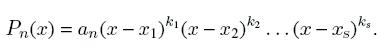
4. Алгебраическое уравнение нечетной степени с действительными коэффициентами всегда имеет хотя бы один действительный корень.
5. Предположим, алгебраическое уравнение с действительными коэффициентами имеет комплексный корень
ξ = α + iβ. Тогда это уравнение так же должно иметь корень η = α - iβ, причем кратности обоих корней одинаковы.
6. Алгебраическое уравнение степени n с целыми коэффициентами ak
не может иметь других рациональных корней, чем несокращаемые дроби p/q, причем p - делитель a0,
и q - делитель an. Если an = 1, тогда все рациональные корни алгебраического уравнения
- целые делители свободного a0 и могут быть легко найдены.
7. Любое уравнение степени ≤ 4 разрешисо в радикалах, что значит, что его корни
могут быть выражены при помощи операций сложения, деления, вычитания и умножения, а так же извлечения корня.
При n ≥ 4 алгебраические уравнения, в основно, в радикалах неразрешимы. Это утверждение носит название теоремы Руффини - Абеля.
8. Теорема Виета. Следующие соотношения между корнями алгебраического уравнения (принимая во внимание
их кратность) и их коэффициенты имеют место быть:
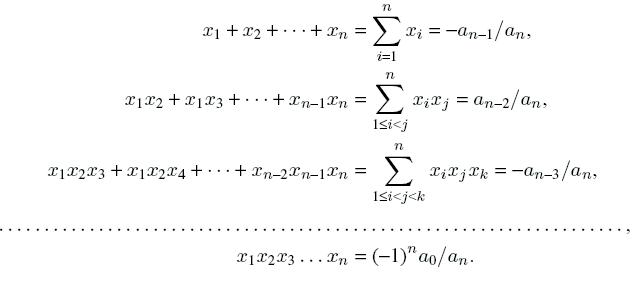
|
| |
|
|