|
|
|
Решение квадратных уравнений с комплексными числами
|
|
Решение квадратных уравнений с комплексными числами
Запишем квадратное уравнение в общем виде:
kx2 + px + q = 0,
где k, p, q - действительные числа. Из курса элементарной математики известно,
что если D > 0, то уравнение имеет два действительных корня, а если D = 0, то один. Случай при D <
0 в элементарной математике не рассматривается, а просто делается вывод, что корней нет.
Однако с использованием комплексных чисел можно доопределить множество решений квадратного
трехчлена при D < 0. Если это так, то будем говорить, что уравнение имеет комплексные корни.
При этом обозначают и корни находят по формуле
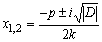
|
| |
|
|