|
|
|
Длина окружности
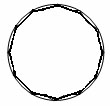
При неограниченном увеличении сторон правильного многоугольника его периметр приближается к периметру окружности.
Теорема
Отношение длины окружности к ее радиусу не зависит от окружности.
Доказательство.
Возьмем две произвольные окружности с радиусами R1 и R2 и длинами l1 и l2. предположим, что
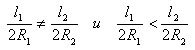
Впишем в окружности правильные n-угольники. N настолько велико, что периметры p1 и p2 правильных многоугольников приближаются к длинам окружностей l1 и l2. Поэтому заменим длины окружностей на периметры, тогда
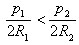
Но периметры правильных выпуклых n-угольников относятся как радиусы описанных окружностей:
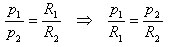
Что противоречит предположению. Теорема доказана.
Отношение длины окружности к диаметру обозначается греческой буквой π.
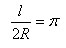
|
| |
|
|