|
|
|
Функции синус и косинус.
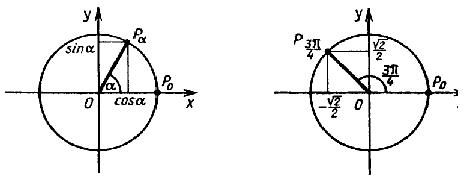
Окружность радиуса r=1 с центром в начале координат называют единичной окружностью.
Пусть точка Pα единичной окружности получена путем поворота точки P0 на
угол α радиан против часовой стрелки. Ордината точки Pα - это синус угла
α, а абсцисса этой точки - косинус угла α.
Далее и везде будем считать, что значения всех углов задано в радианах, если только
специально не указаны другие единицы измерения. Таким образом, если написано
α=1, то подразумевается, что угол α равен 1 рад.
Определение. Числовые функции, заданные формулами y=sin(x) и y=cos(x)
называют соответсвенно синусом и косинусом (обозначают соответсвенно sin и cos).
Область определения этих функций - вся прямая действительных чисел. Область
значения этих функций - отрезок [-1;1]:
D(sin)=D(cos)=R
E(sin)=E(cos)=[-1;1]
Функция sin(x) является нечетной функцией:
sin(-x)=-sin(x)
Функция cos(x) является четной функцией:
cos(-x)=cos(x)
Обе функции sin(x) и cos(x) являются периодическими с периодом T=2π:
sin(x+Tn)=sin(x)
cos(x+Tn)=cos(x), где n - любое целове число.
|
| |
|
|