|
|
|
Функции тангенс и котангенс.
Числовые функции, заданные формулами y=tg(x) и y=ctg(x), называют соответственно
тангенсом и котангенсом (и обозначают соответственно tg и ctg).
Областью определения функции тангенс является множество всех чисел x кроме тех,
где cos(x)=0: x≠π/2+πn, где n - любое целое число.
Областью определения функции котангенс является множество всех чисел x кроме тех,
где sin(x)=0: x≠πn, где n - любое целое число.
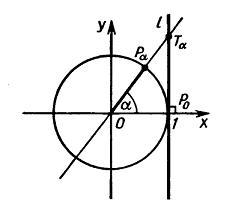
Проведем касательную l к единичной окружности в точке P0. Пусть α -
произволньое число, для тогорого cos(α)≠0. Тогда точка Pα
(cos(α),sin(α)) не лежит на оси ординат, и, следовательно, прямая OPα
пересекает l в некоторой точке Tα с абсциссой 1. Необходимо найти ординату этой точки.
Заметим, что прямая OPα проходит через точки О(0,0) и Pα(cos(α),sin(α)),
поэтому она имеет уравнение y=xtg(α). Абсцисса Tα=1, из вышеприведенного уравнения
прямой находит ординату Tα - tg(α).
Итак, ордината точки пересечения прямых OPα и l равна tg(α). Прямую l
иногда называют линией тангенсов.
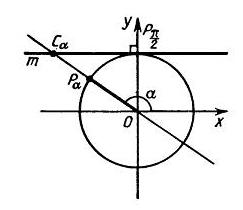
Нетрудно по аналогии показать, что абсцисса точки Cα пересечения прямой OPα
с касательной m к единичной окружности, проведенной через точку Pπ/2, равно ctg(α) при
sin(&alpha)≠0. Прямую m называют линией котангенсов.
Область значений тангенса (котангенса) - вся числовая прямая. Докажем это для функции tg.
Пусть y0 - произвольное действительное число. Рассмотрим точку T(1,y0).
Следуя показанному выше, тангенс угла TOX равен y0. Следовательно, функция tg принимает любое
лействителньое значение.
Функции тангенс и котангенс обладают следующими свойствами:
1. tg(-x)=-tg(x), ctg(-x)=-ctg(x) - функции тангенс и котангенс являются нечетными функциями.
2. tg(x+πn)=tg(x), ctg(x+πn)=ctg(x), n - целое.
|
| |
|
|