|
|
|
Теория по алгебре >> Геометрический смысл приращения. Средняя скорость изменения функции
|
|
Геометрический смысл приращения. Средняя скорость изменения функции
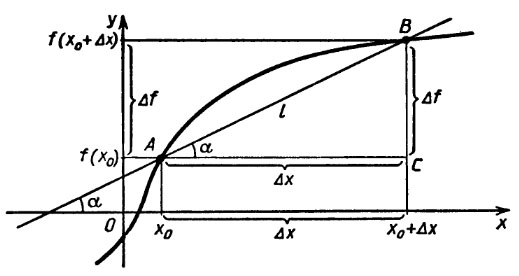
Рассмотрим график функуии y=f(x). Геометрический смысл приращений Δx и Δf (приращение Δf обозначают также Δy) можно понять посмотрев на рисунок.
Прямую l, проходящую через любые две точки графика функции f, называет секущей к графику f. Угловой коэффициент k секущей, проходящей через точки (x0; y0) и (x; y), равен (y-y0)/(x-x0). Его удобно выразить через приращения Δx и Δy.
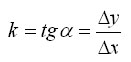
C помощью введеных обозначений приращенийтудобно также выражать среднюю скорость движения за промежуток времени [t0;t0+Δt]. Если точка движется по прямой и известна ее координата x(t), то
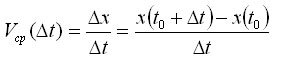
Эта формула верна и для Δt < 0 (для промежутка [t0+Δt;t0]). В самом деле, в этом случае перемещение точки равно x(t0)-x(t0+Δt); длительность промежутка времени равна - Δt, и, следовательно,
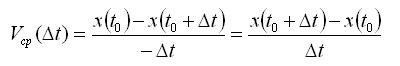
Аналогично выражение
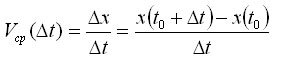
называют средней скоростью изменения функции на промежутке с концами x0 и x0+Δx.
|
| |
|
|