|
|
|
Гомотетия в пространстве
Теорема
Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость ( или в себя при k=1).
Доказательство
Пусть, O – центр гомотетии и α - любая плоскость, не проходящая через точку O. Возьмем любую прямую AB в плоскости α. Преобразование гомотетии переводит точку A в точку A` на луче OA, а точку B в точку B` на луче OB, причем
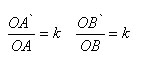
где k – коэффициент гомотетии. Отсюда следует подобие треугольников AOB и A`OB`. Из подобия треугольников следует равенство соответствующих углов AOB и A`OB, а значит, параллельность прямых AB и A`B`.
Возьмем теперь другую прямую AC в плоскости α. Она при гомотетии перейдет в параллельную прямую A`C`. При рассматриваемой гомотетии плоскость α перейдет в плоскость α`, проходящую через прямые A`B`, A`C`. Так как A`B` параллельна AB и A`C` параллельна AC, то по признаку параллельности плоскостей плоскости α и α` параллельны. Теорема доказана
|
| |
|
|