|
|
|
Объем цилиндра
Данное тело имеет объем V, если существуют содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколь угодно мало отличающимися от V.
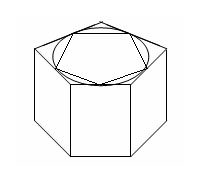
Найдем объем цилиндра с радиусом основания R и высотой H.
Построим две прямые призмы с высотой H такими, что основание одной призмы является n-угольник, содержащий круг, а основание второй призмы n-угольник, содержащийся в круге. Тогда первая призма содержит цилиндр, а вторая призма содержится в цилиндре. При неограниченном увеличении n площади многоугольников приближаются к площади круга S(основанию цилиндра) и, следовательно, их объемы неограниченно приближаются к SH. Тогда

Объем цилиндра равен произведению площади основания на высоту.
|
| |
|
|