|
|
|
Свойства окружности
Теорема.
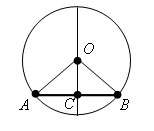
Диаметр окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен ей.
Доказательство.
Пусть AB – хорда окружности и C – ее середина. Треугольник AOB – равнобедренный с основанием AB, так как AO = OB как радиусы. По свойству медианы равнобедренного треугольника, проведенной к основанию, отрезок OC является высотой. Поэтому диаметр окружности, проведенный через середину хорды, перпендикулярен хорде. Теорема доказана.
Теорема.
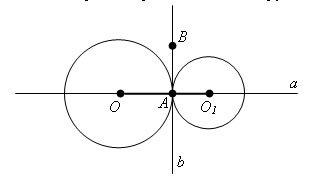
Прямая, проведенная через центры касающихся окружностей, проходит через точку их касания.
Доказательство.
Соединим центры окружностей с точкой их касания. Получим два отрезка OA и O1A.
Через точку A касания двух окружностей проходит общая касательная b к этим окружностям.
Пусть B точка на прямой b. Тогда ∠ BAO1 = ∠ BAO = 90 °.
Следовательно, угол OAO1 – развернутый и точки O, A, O1 лежат на одной прямой a,
перпендикулярной к касательной b. Теорема доказана.
|
| |
|
|