|
|
|
Построение перпендикулярной прямой.
|
|
Построение перпендикулярной прямой
Через точку O провести прямую, перпендикулярную данной прямой a.
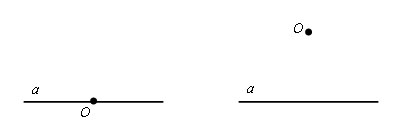
Возможно два варианта:
1. точка O лежит на прямой a;
2. точка О не лежит на прямой a.
Решение.
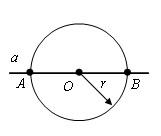
Первый вариант.
Проводим окружность с произвольным радиусом r с центром в точке O. Окружность пересекает прямую в точках A и B.
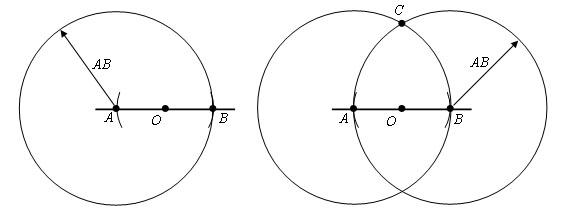
Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей.
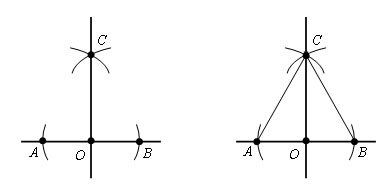
Искомая прямая проходит через точки С и О.
Доказательство.
Проведем отрезки AC и CB. Δ ACO = Δ BCO по третьему признаку равенства треугольников (AO = OB, AC = CB, по построению, CO – общая). ∠ COA = ∠ COB = 90 °. Прямая CO ⊥ AB.
Второй вариант.
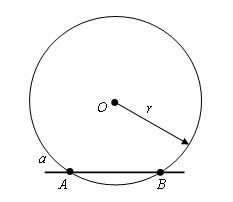
Из точки O проводим окружность некоторым радиусом r, таким чтобы окружность пересекала прямую a. Пусть A и B – точки пересечения окружности с прямой a.
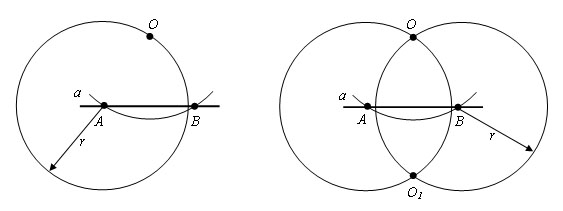
Проведем окружности тем же радиусом r с центрами в точках A и B. Пусть точка O1 – точка пресечения этих окружностей, лежащая в полуплоскости, отличной от той, в которой лежит точка O.
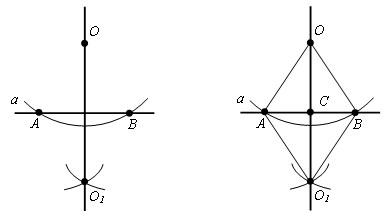
Проведем через точки O и O1 прямую. Это и будет искомая прямая.
Доказательство.
Пусть прямые OO1 и AB пересекаются в точке С. Δ AOB = Δ BO1A по третьему признаку равенства треугольников (AO = OB = AO1 = O1B, по построению, AB – общая). Отсюда следует, что ∠ OAС = ∠ O1AC.
Δ OAC = Δ O1AC по первому признаку равенства треугольников (AO = AO1, по построению, ∠ OAС = ∠ O1AC, AС – общая). Следовательно ∠ OСA = ∠ O1CA, а так как эти углы смежные, то они прямые. Поэтому OC – перпендикуляр, опущенный из точки O на прямую a.
|
| |
|
|