|
|
|
Построение угла, равного данному.
|
|
Построение угла, равного данному
Отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.
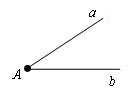
Решение.
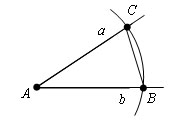
Проведем окружность с произвольным радиусом и центров в вершине A данного угла. Пусть В и С – точки пересечения окружности со сторонами угла. И проведем отрезок BC.
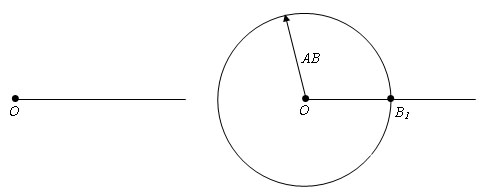
Проведем окружность радиусом AB с центром в точке О – начальной точке данной полупрямой. Точку пересечения окружности с лучом обозначим B1.
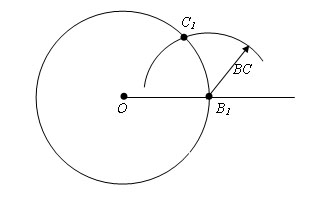
Теперь опишем окружность с центром B1 и радиусом BC. Пусть точка С1 пересечение построенных окружностей в указанной полуплоскости.
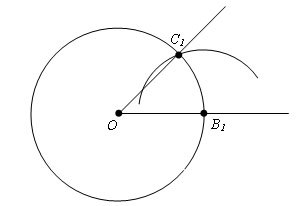
Проведем луч из точки O, через точку С1. Угол C1OB1 и будет искомый.
Доказательство.
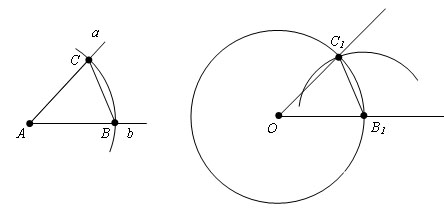
Треугольники ABC и OB1C1 равны как треугольники с соответствующими сторонами. И следовательно углы CAB и C1OB1 равны.
|
| |
|
|