|
|
|
Теория по алгебре >> Преобразования графиков функции. Параллельный перенос вдоль оси ординат.
|
|
Преобразования графиков функции. Параллельный перенос вдоль оси ординат.
В этом разделе будет изложена теория, которая покажет, как из графиков функций y=kx+b (прямая),
y=ax2+bx+c (парабола), y=k/x, y=sin(x) (синусоида), y=cos(x) (синусоида), y = tg(x)
(тангенсоида) и y - ctg(x), применяя известные из курса геометрии сведения о преобразованиях фигур,
строить графики других функций.
Рассмотрим известное нам преобразование, которое называется параллельный перенос на вектор
(0,b) вдоль оси ординат.
Обозначим (x';y') точку, в которую переходит точка с координатами (x;y). Так как перенос осуществляется
вдоль оси ординат, то координаты новой точки будут связаны с координатами старой точки следующим образом: x' = x, y' = y + b.
Возьмем произвольную функцию f с областью определения D(f). Произвольная точка (x; f(x)) графика функции f
переходит в точку (x; f(x)+b). Это означает, что график функции f переходит в фигуру, состоящую из всех точек
(x; f(x)+b), где x принимает все значения и области определения D(f).
Исходя из определения графика функции, эта фигура является графиком функции y=f(x)+b.
Подводя черту под вышеизложенной теорией, сформулируем правило:
Для построения графика функции f(x)+b, где b - постоянное число, надо перенести график функции f на вектор (0,b) вдоль оси ординат.
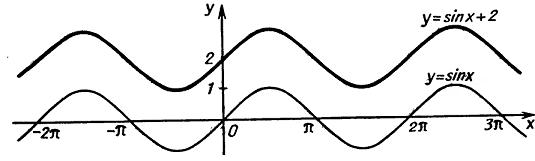
В качестве примера ниже приведен график y=sin(x)+2, который был получен из графика функции y=sin(x) путем переноса на ветор (0,2)
вдоль оси ординат ОУ.
|
| |
|
|