|
|
|
Теория по алгебре >> Производные тригонометрических функций. Формула производной косинуса, тангенса и котангенса.
|
|
Производные тригонометрических функций. Формула производной косинуса, тангенса и котангенса.
Докажем, что функции y = cos x, y = tg x, y = ctg x имеет производные в каждой точке своей области опредления и справедливы формулы:
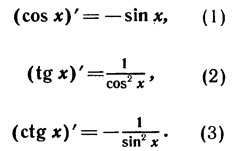
Вывод формулы (1) основан на равенствах
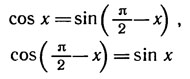
и правиле дифференцирования сложной функции:
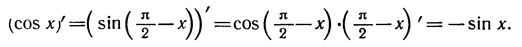
Чтобы доказать справедливаость формул (2)и (3), применим формулу для нахождения производной частного и выведенные формулы производной синуса и косинуса (1):
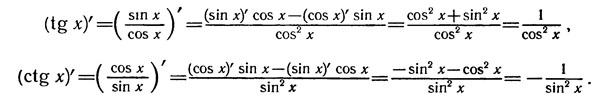
|
| |
|
|