|
|
|
Сечение конуса плоскостями
|
|
Сечение конуса плоскостями
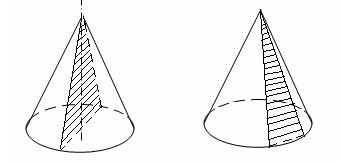
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса
Теорема
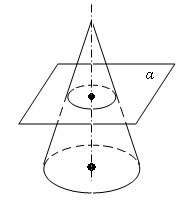
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.
Доказательство
Пусть α – плоскость, параллельная плоскости основания конуса и пересекающая конус. Преобразование гомотетии относительно вершины конуса, совмещающее плоскость α с плоскостью основания, совмещает сечение конуса плоскостью α с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. Теорема доказана.
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший кусок. Оставшаяся часть называется усеченным конусом.
|
| |
|
|