|
|
|
Сечение шара плоскостью
Теорема
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Доказательство
Пусть α - секущая плоскость и O – центр шара. Опустим перпендикуляр из центра шара на плоскость α и обозначим через O` основание этого перпендикуляра.
Пусть X – произвольная точка шара, принадлежащая плоскости α. По теореме Пифагора
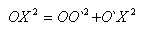
Так как OX не больше радиуса R шара, то
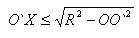
т.е. любая точка сечения шара плоскостью α находится от точки O` на расстоянии, не большем
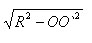
следовательно, она принадлежит кругу с центром O` и радиусом
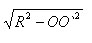
Обратно: любая точка X этого круга принадлежит шару. А это значит, что сечение шара плоскостью α есть круг с центром в точке O`. Теорема доказана.
|
| |
|
|