|
|
|
Симметрия шара
Теорема
Любая диаметральная плоскость шара является его плоскостью. Центр шара является его центром симметрии.
Доказательство
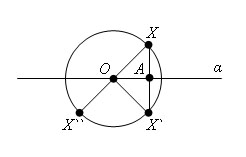
Пусть α - диаметральная плоскость и X - произвольная точка шара. Построим точку X`, симметричную точке X относительно отрезку XX` и пересекается с ним в его середине. Из равенства прямоугольных треугольников OAX и OAX` следует, что OX` = OX.
Так как OX ≤ R, то и OX` ≤ R, т.е. точка, симметричная точке X, принадлежит шару. Первое утверждение теоремы доказано.
Пусть теперь X`` - точка, симметричная точке X относительно центра шара. Тогда OX`` = OX ≤ R, т.е. точка X`` принадлежит шару. Теорема доказана полностью.
|
| |
|
|