|
|
|
Возрастание и убывание функций.
Познакоимимся на примере с возрастанием и убыванием функции. На рисунке ниже
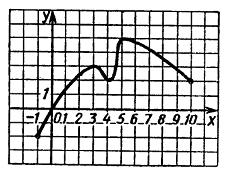
изображен график функции, определенной на отрезке [-1;10]. Эта функция возрастает на
отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].
Рассмотрим еще один пример. Очевидно, что функция y=x2 убывает
на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что
график этой функции при изменении x от -∞ до 0 сначала опускается до нуля,
а затем поднимается до бесконечности.
Определение. Функция f возрастает на множестве P, если для любых x1 и
x2 из множества P, таких, что x2>x1, выполнено
неравенство f(x2) > f(x1).
Определение. Функция f убывает на множестве P, если для любых x1 и
x2 из множества P, таких, что x2>x1, выполнено
неравенство f(x2) < f(x1).
Иначе говоря, функция f называется возрастающей на множестве P, если большему значению
аргумента из этого множества соответствует большее значение функции. Функция f называется
убывающей на множестве P, если большему значению аргумента соответствует меньшее значение
функции.
|
| |
|
|