|
|
|
Теория по алгебре >> Производные тригонометрических функций. Формула производной синуса.
|
|
Производные тригонометрических функций. Формула производной синуса.
Докажем, что функция синус имеет производную в любой точке u
(sin x)’ = cos x.
Применяя формулу
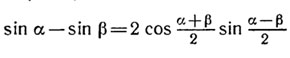
находим
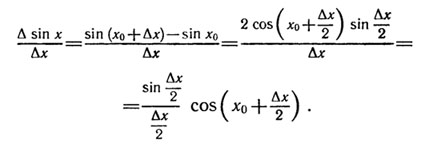
Для вывода формулы достаточно показать, что:
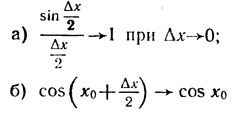
при Δx→0.
Опираясь на эти утверждения, можно получить формулу (1). Действительно, при Δx→0
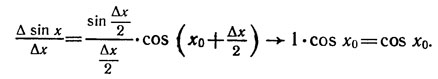
Утверждения а) и б), на которые мы опирались выше, имеют наглядный геометрический смысл.
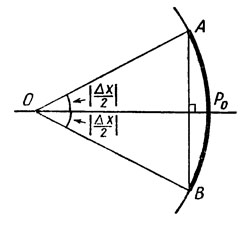
а) Отложим на единичной окружности от точки Р0 в обе стороны дуги Р0А и Р0В длиной |Δx|/2 (рис. сверху) Тогда длина дуги АВ равна |Δx|, а длина хорды AВ равна 2|sin (Δx/2)|. При малых |Δx| длина хорды АВ практически не отличается от длины стягиваемой ею дуги АВ. (Этим фактом вы уже пользовались в курсе геометрии при выводе формулы длины окружности. Действительно, при больших n верно, как известно, приближенное равенство Рn≈С, где Рn — периметр правильного вписанного n-угольника, а С — длина окружности. Значит, длина стороны такого многоугольника приближенно равна длине дуги, которую эта сторона стягивает.) Следовательно,
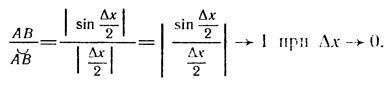
б) Заметим, что длина хорды АВ меньше длины дуги АВ, т. е.
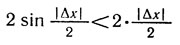
Воспользовавшись формулой разности косинусов и этим неравенством, находим:
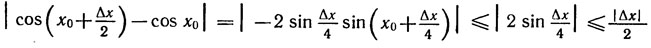
Но |Δx|/2→0 при Δx→0. Поэтому
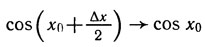
при Δx→0.
|
| |
|
|